线段树：竞赛数据结构的基石

无论是纯粹的数据结构题还是数据结构优化其他算法，线段树都是绕不开的一个东西。

线段树的基本思想事实上十分简单：分治。把大区间拆成小区间，能延迟操作就延迟操作，这就是线段树的基本思想。它解决的问题也很简单：区间查询，区间修改。

在数据结构题以外，我们依然可以见到线段树的身影，包括但不限于树剖维护树上问题、优化dp状态转移、优化dijkstra等。这些我们都将在下面见到例题。

当然，在面对一些其他问题时，线段树的功能就有些捉襟见肘了，这种时候我们通常会考虑另一个几乎万能的数据结构：平衡树。当然平衡树也不是真的万能，有些问题（例如在线带修改区间第k大）单独的平衡树和线段树都无法解决，于是我们又会请出重量级的数据结构：树套树。不过，这些都超出了我们现在的讨论范围。这篇文章的重心依然会放在线段树上。

最简单的线段树1就不赘述了。我相信在座的各位都可以十分流畅的写出一颗支持基础操作的线段树。至于线段树2，我们将在后面的双半群模型部分详细讨论这个问题及其加强版。

这里提一个建议：找到一个自己最喜欢的线段树的写法，然后就一直沿用这个写法，这样考场上不容易写错。

关于线段树基础的补充：

考虑到在座的各位可能并不能顺利的切掉线段树模板题，因此加入一个对线段树的基本介绍。

顾名思义，线段树首先得是一棵树，并且是一颗二叉树。在这棵二叉树的每一个节点上，维护了一个区间的信息，具体什么信息视题目情况而定，这里以区间和为例。这棵树是长成这个样子的：

纯手绘，丑的要命

先考虑区间查询。自然，为了优化时间复杂度，在树上查询的时候我们不可能递归到叶子节点上去查询。

考虑查询区间和节点区间之间的关系。注意到，如果一个节点的区间被完全包含了，那么查询他的子树就是完全没有必要的。因此，我们可以直接返回这个节点上维护好的区间信息，从而优化时间复杂度。而如果查询区间没有完全覆盖当前节点区间，则递归查询左右子树（如果有交集的话），然后将两边的结果合并。

换个角度，也可以说是将查询区间拆分为若干个节点区间，并且这些区间的个数是 $O(\log n)$ 的，从而实现 $O(\log n)$ 复杂度的区间查询。

接着，考虑单点修改。单点修改非常简单，一路深搜到对应的叶子节点进行修改即可。然而，单点修改的过程中，路上经过的节点的区间和也会随着这次修改而改变。因此我们需要一个 pushup 操作，用于在更新完子树信息之后，维护当前节点的区间信息。这个操作显然是常数复杂度，不会影响总复杂度，因此总复杂度依然是美丽的 $O(\log n)$。

最后考虑区间修改。延续我们在区间查询的思想，能覆盖优先覆盖。如果一次区间修改操作完全覆盖了某一个节点的区间，那么我们就直接修改这个区间上的区间信息（在这里就是区间和）。例如，我们要做区间增加 delta 的操作，而 p 这个节点被完全覆盖了，那么我们就可以直接做 p.sum += delta * p.len 从而快速修改区间信息。

然而这样会带来一个问题。如果在修改了 p 之后需要查询 p 的子树信息，显然按照刚才的操作， p 的子树没有任何改变，这显然是不对的。因此，我们引入一个重要的东西叫做懒标记 tag，记录 对当前节点做过哪些操作。这样，当我要访问 p 的子节点的时候，我就可以知道 p 区间里的每一个子节点都加上了 delta ，从而在查询 p 的子树的时候可以正确的维护他们的信息。

具体的讲，我们引入一个操作叫做 pushdown ，表示将 p 的标记下传到他的子结点上，并且清空自己身上的标记。那么在 pushdown 的时候，我们就会做两个操作：维护子节点的 sum，然后更新子节点的 tag。具体的操作视题目而定。

这样就可以顺利的入门线段树了！（喜）

基础题：

【模板】线段树1

【TJOI2018】数学计算

稍进阶一些的题：

【模板】线段树2

P4145 上帝造题的七分钟

P1471 方差

【SCOI2010】序列操作

【NOI Online #1 提高组】 冒泡排序

标记永久化：替代标记下传

在传统线段树中，面对区间操作，我们常常使用懒标记的方式进行维护。当我们对一个做了懒标记的节点的子节点进行操作的时候，常常需要使用 pushdown 的方法下传标记，使子节点的 val 和 tag 处于一个正确的状态。然而，出于空间或者时间或者代码复杂度的考虑，有时候下传标记并不可行，这个时候便有了标记永久化的技术，可以代替标记下传。

标记永久化的思想是这样的：我们把标记放在每个节点上，修改的时候不下传，查询的时候累加路过的所有的标记，从而实现和标记下传一样的效果。

这个思想将在处理zkw线段树、李超线段树和可持久化线段树的时候用到。

离散化：缩小定义域的有效手段

有些时候我们会遇到一些问题，这些问题需要处理相当大的区间，然而可能访问到的节点数并不太多。这种时候我们会使用离散化的手法来处理。

离散化的手法很多，最常见的是 sort 和 unique 的手法。首先将序列排序，然后用 unique 去除连续的重复元素，最后 lower_bound 二分查找对应位置，从而缩小定义域。

权值线段树：建立在值域上的线段树

权值线段树本质上和一颗普通的线段树并没有什么不同，他就是一颗线段树。不同的是，权值线段树建立在值域上。

从一个简单些的例子开始，这是一个经典例子：求序列的逆序对个数。

这个题目有两个经典做法：归并排序和树状数组。我们讨论的就是树状数组的做法。自然，树状数组能做的事情线段树都能做，因此我们可以将树状数组看作线段树的一种实现方式，从而讨论线段树上的问题。

这里树状数组的做法就是所谓的权值树状数组。在计算逆序对之前先将序列离散化，得到序列中元素个数为tot。然后建立大小为tot的树状数组，从左往右扫，扫到s[i]则将树状数组中小于等于s[i]的位置加一，并且查询大于等于s[i]的树状数组上的和，从而得到s[i]对总逆序对数的贡献。

容易发现，我们这里的树状数组中，每一位描述的并不是s中某一位的值，而是某一个值所对应的内容。换句话说，这个树状数组中每个位置描述的是一个桶，类似于桶排序。

当然，单纯的权值线段树能做的事情其实并不多，但是如果将权值线段树持久化，则可以实现很多神奇的功能，例如在线区间第k大。这是一个经典例题，我们将会在后面主席树的部分（如果讲的到的话）详细讲解。

扫描线：离线化处理区间问题

扫描线最早是解决一些几何问题的：

【模板】扫描线

求 $n$ 个四边平行于坐标轴的矩形的面积并。

做法很简单：把每个矩形垂直于x轴的边放入一个结构体，并记录这是矩形的左边界还是有边界，然后以对应的横坐标排序。举个例子，对于顶点分别在(x1,y1)和(x2,y2)的一个矩形，我们建立两个结构体，分别是(x1,y1,y2,1)和(x2,y1,y2,-1)。

接下来，从左往右扫，每扫到一个(x,y1,y2,t)的结构体，则将线段树上在[y1,y2]区间的节点加上t，并且维护区间上值为正的节点个数。这么做相当于把这一堆矩形的并按照不同的x切开，变成一片一片的小矩形处理。如下图（图源OI-wiki）：

图源OI-wiki

那么，我们的线段树其实就是在维护每一小片矩形的边长，然后求面积并。

从这个问题可以很直接的衍生出一些很相似的几何问题，例如矩形周长并，二维数点等。这些可以留作课后练习。

接下来要加速了！

事实上，扫描线的功能远远不止几何问题。面对许多区间询问的问题，我们同样可以用扫描线的思想来处理。这种做法的核心在于：把一个静态的区间查询问题，变成一个动态的区间查询问题。乍一看这样似乎是把问题复杂化了，然而很多时候维护动态区间查询的难度远远小于静态区间查询。

举个例子，P8868 比赛。题意如下：

给定两个长为 $n$ 的序列 $a,\ b$，每次询问给定 $l,\ r$，求：对于所有的 $l\le p \le q \le r$，区间 $[p,\ q]$ 上 $a,\ b$ 的最大值 $m,\ n$ 的乘积之和。

形式化地说，求： $ \sum^r{p=l} \sum^r{q=p} (\max^q{i=p}a_i) \cdot (\max^q{i=p}b_i) $

这是一道不那么经典但是很近的数据结构真题。我们会在后面的双半群模型的部分再次提到它。显然，他是一个静态的区间查询问题。

我们离线记录每一组询问(l,r)，然后以右端点升序排序。接下来，维护两个单调栈，得到la和lb两个数组，la[i]表示：以i为右端点且最大值为a[i]的区间的最小左端点。lb同理。显然这个用单调栈很好处理。

那么，当我们从左往右扫过每一个r的时候，从la[i]到i区间的最大值是会更新的，换句话说就是变成了一个区间覆盖问题。从而问题转化为了区间历史和问题。相比起直接维护原来的问题，这个问题变得简单很多。

当然，区间历史和依然是一个麻烦的问题。我们将会在双半群模型的部分进一步探讨如何处理这道题。

还有一道近年真题是P9871 天天爱打卡，这是一道扫描线+树状数组优化dp的问题，相比起P8868简单许多，可以留作习题。

动态开点线段树：优化空间

其实动态开点线段树和普通线段树并没有本质上的区别。传统线段树的lson和rson只是把它看作一个完全二叉树。而只要我们像建一棵普通二叉树一样建线段树，就可以得到动态开点线段树。

动态开点线段树的好处就是可以降低空间消耗，这样在处理一些空间比较紧张的题目时就可以防止MLE。

zkw线段树：循环优化线段树

这是一个神奇的数据结构，有点类似树状数组。

首先，我们考察一棵传统线段树的结构。注意到，传统线段树里，数据总是存在叶子节点上的。如果恰好，我们的数据总量是二的幂，那么这棵树就会变成一棵满二叉树，这是线段树空间利用率最高的情况。这个时候考察数组中每个元素的位置与叶节点的编号位置，容易注意到：两者的差值是一个定值。这种情况下，线段树的许多操作可以被循环化。

然后，众所周知，循环的常数是小于递归的。因此，我们考虑，能不能通过这种方式使用循环代替线段树操作中的递归。

首先，根据前面所说的结论，建树的过程是显然的。只需要把原数组的内容放到线段树中对应叶节点的位置即可。代码很显然。这里我们可以看到zkw线段树的一个核心思想：自底向上。

1
2
3
4
5
6
7
8
void build() {
  for (int i = 1; i <= n; ++i) {
    segt[n + i].val = val[i];
  }
  for (int i = n; i >= 1; --i) {
    segt[i].val = segt[i * 2].val + segt[i * 2 + 1].val;
  }
}

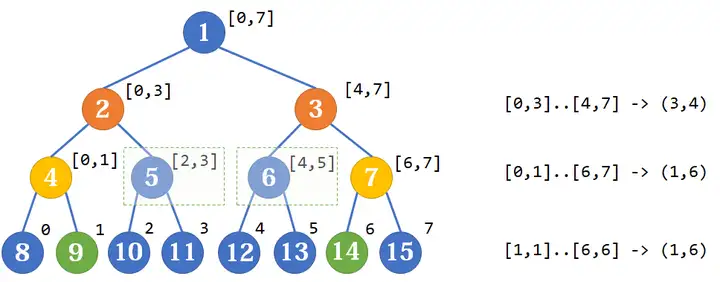
然后考虑区间查询。假设我们要查询 $[l,r]$ 区间的和，我们将其转化成 $(l-1,r+1)$ 开区间处理。例如，在这棵树里，如果我们查找 $[2,5]$ 的区间信息，我们就可以设置两个指针 p=1 和 q=6 ，然后分别向上跳，直到两者有相同的父亲。显然，一个节点的父亲编号是自己编号的一半。这个时候我们可以感性地注意到，跳的路径会围出来树上的一个区间，这个区间就是要查询的区间。事实上，跳的过程就是将边界上的点排除到答案之外的过程。接着模拟，我们会发现：当左指针是左儿子，或者右指针是右儿子的时候，这个指针对应的兄弟节点的子树就是答案的一部分。而判定左右儿子的过程只需要判断当前节点的奇偶性即可。

图源知乎

接着考虑区间修改。很显然，在 zkw 线段树的自底向上过程中，我们是没有办法进行标记下传的，这个时候就需要应用标记持久化的思想了。区间修改的过程大体上和区间查询是类似的，但是注意：修改过程会对所有的父节点都造成影响，因此需要一直跳到根节点。同样，因为标记持久化的原因，查询也需要向上跳到根节点。

最后是半封装的模板，只需修改三个 merge 以及对应的 Info 和 Tag 即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const ll MAXN = 100010;
struct Node {
  struct Info {
    ll val, len;
  } info;
  struct Tag {
    ll add;
  } tag;
};
ll lowbit(ll x) { return x & (-x); }
ll n, m, n0;
ll val[MAXN * 2];
Node segt[MAXN * 2];
Node::Info merge(Node::Info lhs, Node::Info rhs) {
  return Node::Info{lhs.val + rhs.val, lhs.len + rhs.len};
}
Node::Info merge(Node::Info info, Node::Tag tag) {
  return Node::Info{info.val + info.len * tag.add, info.len};
}
Node::Tag merge(Node::Tag pre, Node::Tag cur) {
  return Node::Tag{pre.add + cur.add};
}
void pushup(int cur) {
  segt[cur].info = merge(segt[cur * 2].info, segt[cur * 2 + 1].info);
  segt[cur].info = merge(segt[cur].info, segt[cur].tag);
}
void build() {
  for (int i = 1; i <= n; ++i) {
    segt[i + n].info = Node::Info{val[i], 1};
  }
  for (int i = n; i >= 1; --i) {
    pushup(i);
  }
}
void update(int l, int r, Node::Tag tag) {
  int p = l + n - 1, q = r + n + 1;
  for (; p / 2 != q / 2; p >>= 1, q >>= 1) {
    if (p < n) {
      pushup(p);
      pushup(q);
    }
    if (p % 2 == 0) {
      segt[p ^ 1].info = merge(segt[p ^ 1].info, tag);
      segt[p ^ 1].tag = merge(segt[p ^ 1].tag, tag);
    }
    if (q % 2 == 1) {
      segt[q ^ 1].info = merge(segt[q ^ 1].info, tag);
      segt[q ^ 1].tag = merge(segt[q ^ 1].tag, tag);
    }
  }
  for (; p; p >>= 1, q >>= 1) {
    pushup(p);
    pushup(q);
  }
}
Node::Info query(int l, int r) {
  int p = l + n - 1, q = r + n + 1;
  Node::Info linfo = {0, 0}, rinfo = {0, 0};
  for (; p / 2 != q / 2; p >>= 1, q >>= 1) {
    linfo = merge(linfo, segt[p].tag);
    rinfo = merge(rinfo, segt[q].tag);
    if (p % 2 == 0) {
      linfo = merge(linfo, segt[p ^ 1].info);
    }
    if (q % 2 == 1) {
      rinfo = merge(rinfo, segt[q ^ 1].info);
    }
  }
  for (; p; p >>= 1, q >>= 1) {
    linfo = merge(linfo, segt[p].tag);
    rinfo = merge(rinfo, segt[q].tag);
  }
  return merge(linfo, rinfo);
}
int main() {
  ll op, u, v, w;
  ios::sync_with_stdio(false);
  cin >> n >> m;
  n0 = n;
  for (int i = 1; i <= n0; ++i) {
    cin >> val[i];
  }
  while (n != lowbit(n))
    n += lowbit(n);
  build();
  for (int i = 1; i <= m; ++i) {
    cin >> op >> u >> v;
    if (op == 1) {
      cin >> w;
      update(u, v, Node::Tag{w});
    } else if (op == 2) {
      cout << query(u, v).val << endl;
    }
  }
  return 0;
}

线段树上二分：替代平衡树

在一棵动态开点的权值线段树上，可以通过树上二分的方式替代平衡树的一些基础功能。

然而相比之下可能FHQTreap更好写一点

举个例子：线段树上查找第 k 大。显然，如果使用权值线段树的话，这个问题就变成了：在线段树上二分找到一个点，这个点上前缀和为 k。

考虑进行深搜，深搜的时候考察左右子树的和，从而判断 k 的位置哪一侧。如果 segt[lson].val >= k，意味着在左边，递归左子树查找；否则，k -= segt[lson].val 然后递归右子树。这个过程和平衡树上的操作是完全一样的。

习题：普通平衡树

李超线段树：处理平面上的线段问题

李超线段树解决了这样的一个问题：

在平面直角坐标系下，在线维护以下两类操作：

  1. 加入一条线段

  2. 给定一个横坐标k，然后求所有线段中横坐标为k且纵坐标最大的一个的编号

先考虑直线的情况。我们在线段树上的每一个节点上存一条直线（事实上是它的编号），表示：所有直线中，横坐标为这个节点的 mid 处纵坐标最大的直线。

之所以是 mid 处最大而不是整个区间都最大，是因为显然可能存在整个区间不同部分最大值不是同一条直线的情况。我们使用 mid 处最大的直线代表这个区间，便于后续处理操作。这里利用了标记持久化的思想，这个做法我们会在可持久化线段树的区间操作上再次看到。我们到后面再说。

那么我们考虑如何将两条直线合并。如图。

我们有两条直线 $f$ 和 $g$ ，其中 $f$ 是新线段。考虑中点 $m$ 处的大小关系。如果 $f$ 优于 $g$ 则将两者交换。那么考虑 $f$ 不如 $g$ 的情况。此时考察左右端点。

  1. 如果左端点处 $f$ 更优而右端点处不是，则在左半部分存在交点。换句话说，在左子树上有一些节点是需要用 $f$ 来更新的。这个时候递归到左子树更新节点。

  2. 右端点处 $f$ 更优，同理递归右子树。

  3. 都不更优，则 $f$ 在这个区间不会成为答案，直接返回。

此时就完成了两条直线的合并操作。

接下来考虑线段。线段是直线限制定义域后的产物。我们可以将前面加入直线的操作看作是加入了一条定义域是 $[1,\ n]$ 的线段。联想一般线段树进行区间修改时的操作，我们会把修改区间拆分成 $O(\log n)$ 个小区间，分别进行区间覆盖操作。同样我们在这里也这么做，把线段的定义域拆分成 $O(\log n)$ 个小区间，在这些区间里这条线段是完全覆盖的，从而可以沿用此前直线的做法。因此总的复杂度是 $O(\log^2 n)$ 的。

至此，我们完成了修改操作。接下来需要考虑查询操作。

考虑一般线段树的单点查询操作，我们在线段树上递归找到对应的节点，直接返回对应的值。然而这时考虑如下情况：

此时橙色线段的覆盖操作只更新了红色节点，而没有更新绿色节点。此时在我们递归找到绿色节点时就会得到错误的答案。这是因为，我们前面拆分线段的操作本质上是对对应节点的懒标记，但是我们并没有给出一个合适的方式 pushdown 。这个时候就需要应用标记持久化的思想：我们在递归向下找节点的时候，记录每一个节点上的线段在 k 时的最大值。这样即可得到正确的答案。

模板题：【HEOI2013】Segment

Segment Tree Beats：对传统线段树的功能扩展

模板题：线段树3

这种线段树变体的系统论述最早开始于国家集训队的一篇论文，在CodeForces上的一篇帖子亦有论述。他解决的问题如下：

维护一个数据结构，在线维护以下操作：

  1. 求区间最值

  2. 求区间和

  3. 区间加法

  4. 区间 $\min:\ \forall i \in [l,r],\ a_i = \min(a_i,k)$

首先考虑没有操作 4 的情况。这个时候显然就是一个很普通的线段树模型。

那么我们考虑操作 4 。区间取 $\min$ 并不是一个很好处理的事情，因为它不满足线段树模型在群论上的一些性质（也就是说难以构造一个双半群模型）。这个时候我们曲线救国：考虑能否将这个操作转化为一个更好实现的操作，比如区间加减或区间赋值等。这个时候就需要改变线段树的更新策略了。正常来讲，我们递归到一个被完全区间覆盖的节点时就会放下懒标记，但此时我们要进一步向深处递归，直到节点满足一些更强的限制条件。

此时容易有两个思路：

  1. 记录区间最大值和次大值，如果次大值小于 k ，则对最大值做区间减法。

  2. 记录区间最大值和最小值，如果最小值大于 k ，则做区间赋值。

看起来两者皆可，但后一种做法的复杂度事实上是不太正确的。因此着重考虑前一种做法。

在对最大值和非最大值分别操作的时候，需要维护两套标记，分别维护对最大值的加减法和非最大值的加减法。同时我们还需要维护区间次大值和区间里最大值的个数。总的复杂度是 $O(n\log^2n)$ 的。复杂度证明比较复杂，建议参考 CodeForces 上的那篇帖子。

具体代码实现并不复杂，留做习题。

可持久化线段树/主席树：保存所有历史版本的线段树

见隔壁文章：主席树

线段树合并/分裂：处理多棵权值线段树的有力工具

事实上，线段树的合并和分裂与无旋treap的 split 和 merge 操作很像。

首先考虑合并 merge，并且考虑在动态开点树上的 merge 操作。我们定义 merge 的返回值是合并后的树根，合并的过程就是在两棵树上同步深搜的过程。如果两棵树有一棵为空，则返回非空节点；否则分别合并两棵树的子树，然后变为当前节点的新子树返回。这个过程和无旋 treap 的合并过程如出一辙。

接着考虑分裂 split。

线段树的应用：图论与动态规划等

这里讲几个经典的例子。

RMQ

非常显然，不再赘述。

区间历史最值

注意：区间历史最值和持久化是两码事情，绝不可以混为一谈。 区间历史最值指的是，在每一个位置上所有曾经出现过的数中的最值。

显然，我们既需要维护当前树上每个节点表示区间的区间最值，还需要维护这个区间的历史最值。接下来考虑区间加法，很明显，我们需要维护每个区间的加法标记，这是常规的。那么就考虑区间加法对历史最大值的影响了。

想象一下，我们在对一个节点进行反复的加减操作（注意，是一个节点而非一个区间）。那么这个区间的最大值也随着在加加减减的变化。但是历史最大值只要考虑每次操作后最大值的最大值即可，换句话说并不是每次 tag 的变化都要更新历史最大值。显然的，只有 tag 最大的时候需要更新历史最大值。那么我们只要在每次更新 tag 的时候再维护一个 tag 的最大值， pushdown 的时候把两个标记一块下传即可。

模板题（也是Segment Tree Beats的模板题） 线段树 3

线段树优化 Dijkstra 算法

其实非常简单。

考察一般做堆优化 Dijkstra 时的做法。每次从堆中取出 dis 最小的元素，把它从堆中弹出并固定它的 dis，然后对它的所有相邻节点做松弛操作并放进堆里（或者直接修改堆中内容然后 pushup）。

我们在这棵树的节点编号上建立一棵线段树。那么，每次从堆中取最小元素相当于在线段树中取整个区间的最小值所在位置的编号，把它弹出堆相当于将其在线段树中的权值修改为 INF 使它在后续不再可能成为最小值，松弛则是修改其邻接点在线段树中的权值。这个过程如果理解了将会十分自然。本质上就是用线段树实现了堆的功能。

这个做法的复杂度是 $O(m\log n)$ ，和手写堆优化一样。

不过这个做法只能作为一个玩具。我以前做的一个性能测试显示，在不开 O2 时手写堆优略胜 STL 一筹，在开了 O2 时 STL 堆性能一骑绝尘，远超 pbds 和线段树等技法。（以及无论是否开了 O2，在随机图上 SPFA 的性能都强于 Dijkstra。当然，仅限随机图）因此不建议在考场上使用这个做法，但是可以以此作为线段树的一个练手题目。

线段树处理静态树上路径/子树问题

线段树处理静态树上问题时，需要借助另一个十分强大的工具：树链剖分。当然，树剖有很多剖发，常见的有两种，重链剖分和长链剖分，前者通常与线段树结合，而后者则通常用于优化树形dp。

这里插播一则关于重链剖分的简单介绍。

树剖并没有他听起来的那么难（事实上我认为他比树上倍增好写得多）。简单概括，树剖只需要进行两次 dfs 的操作，即可将有时难以处理的树上问题变成一个较为简单的序列问题，从而允许我们使用线段树等处理序列问题的工具来处理树上问题。

树剖的流程大体上分成这样几步：

  1. 寻找重子：找到每个节点最重的一个儿子。在重链剖分中我们定义一个节点的重量是以它为根的子树的节点个数，在长链剖分中则定义为这棵子树的深度。多个最大值任取一个。

  2. 记录 dfn 序：对于每个节点，先搜重子，再搜其它儿子，记录下此时每个节点的次序。

容易发现，除了叶子节点外，每个节点都有且只有一个重子。假如我们只留下树上连接一个节点和它的重子的边，那么这棵树便会成为许多个链。这便是所谓的树链剖分。我们把连接重儿子的边称作重边，剩下的边称作轻边。

接下来我们考察这个 dfn 的性质。

首先，对于任意的 dfn 都有一个性质：一棵子树中的所有节点的 dfn 是连续的。

接着，我们考察这个 dfn 的特殊性质。由于每次深搜时都优先重子，因此可以发现，一条重链上的节点的 dfn 都是连续的。这是非常重要的一个性质。正是因为这个性质，树剖可以维护树上路径信息。我们记 top[u] 为 u 所在链上深度最小的节点编号（不是dfn），记 fa[u] 为 u 的父亲节点编号。

然后我们考察时间复杂度。首先给出结论：从任意一个节点到根节点，经过的轻边数量是 $O(\log n)$的。证明如下：

考察每次跨过一条轻边的情况。记这条边是 (u, v)，那么显然，u 有一个重儿子 prefer[u]，其大小是大于等于 v 的。那么，u 的大小至少是 v 的大小的两倍。每次条轻边都会使这颗树的大小的下界翻倍，从而总的跳轻边次数最多是 $O(\log n)$。这也是为什么必须找重儿子而不是随意的一个儿子来剖分。

到现在为止，我们已经成功的获得了 dfn 数组，相当于构造了一个从树上节点到线性序列的双射。这为我们使用线段树维护树上问题开辟了道路。

事实上，如果把眼光放的更广阔些，可以发现把树上节点映射到一个序列的元素是处理树上问题的一个相当好用的思路。只要涉及到了树上的子树查询修改与路径查询修改，那么就一定可以用树剖+数据结构的思路解决。当然他也有限制，树剖只能解决静态问题（不加减边和点），那么假如我还要在树上动态加边删边怎么办呢？我们可以用功能更强大的平衡树维护。——这便是大名鼎鼎的 Link-Cut Tree 的雏形了。

其实到目前为止，线段树如何维护树上路径/子树问题已经很明朗了。假如我们需要对树上 (u, v) 的路径进行修改，那么我们按照以下步骤操作：

  1. 找到两个点对应的 top 与 dep。这里假定 dep[top[u]] > dep[top[v]]。否则 swap(u, v)

  2. 对 [dfn[top[u]], dfn[u]] 做区间操作，然后令 u = fa[top[u]]。这个操作相当于一次性跳到链顶后跳过那条轻边。

  3. 判断 top[u] == top[v]。成立则结束，否则继续 1 2 的操作。

根据前面的结论，2 的操作最多是 $O(\log n)$ 次。如果我们用线段树来维护这个区间操作，那么总的时间复杂度就是 $O(\log^2 n)$。这个复杂度已经可以满足绝大多数需要了。

子树操作同理。我们在第二次深搜的时候记录每个节点子树中最大的 dfn 即可，记为 btn。那么对 u 为根的子树进行操作相当于对 [dfn[u], dfn[btn[u]]] 做区间操作。时间复杂度 $O(\log n)$。

习题：

【模板】轻重链剖分

【Vani有约会】雨天的尾巴 // 注：这个题也是线段树合并的板子，但是如果用树剖则不需要使用线段树合并

【NOI2015】软件包管理器

李超线段树处理斜率优化

这里插播一则斜率优化的简单介绍

斜率优化处理的是这样的一类最优化 dp，它的方程可以化成这样的形式：$bi = \max{j<i}{y_j-k_ix_j}$ 的形式。容易发现，这种情况下可以用线性规划的方法优化这个 dp 过程，从而将状态转移转化为一个计算几何问题，然后用解决凸包的问题快速转移。

但是这个凸包问题是动态的，意味着我们需要动态加点求凸包。对于一些 $k_i$ 具有单调性的问题而言，可以用 deque 方便的解决，而如果不具有单调性则需要使用平衡树或cdq分治等繁琐的方式来实现动态凸包。李超树本质上也是求解动态凸包的一个工具，因此同样可以用于求解斜率优化。

普通的斜率优化是将状态转移方程转化成 $bi=\max{j<i}{yj-k_ix_j}$ 的形式，然后把斜率为 $k_i$ 的直线从下往上移动直到和凸包相切；而对于李超线段树则是常把状态转移方程转化为 $y_i=\max{j<i}{k_jx_i+b_j}$ 的形式。容易看到这两种形式在事实上是等价的。

具体而言，每次转移之后求得对应的 $k_i$ 和 $b_i$ ，然后将这条直线加入到李超树中，每次转移的时候在李超树中查询 $x_i$ 对应的最大直线/最小直线，进行状态转移，从而将 $O(n^2)$ 的dp过程优化到 $O(n\log n)$。

例题：【SDOI2012】任务安排

首先考虑 dp 方程。令 $dp_i$ 为取前 $i$ 个任务且结束的最小开销，容易得到 dp 方程：

接下来重新处理这个方程，得到这个形式：

显然变成了一次函数的形式。接下来在 $sumt$ 上建立李超线段树。注意，询问点只有 n 个，因此需要做离散化，使得空间开销落在可以接受的范围。

完整代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define lson (cur * 2)
#define rson (cur * 2 + 1)
const ll MAXN = 300010;
ll n, s;
ll t[MAXN], c[MAXN];
ll sumt[MAXN], sumc[MAXN];
ll k[MAXN], b[MAXN];
ll unisumt[MAXN], pos[MAXN], tn;
ll segt[MAXN * 4];
ll dp[MAXN];
ll calc(ll id, ll x) { return k[id] * unisumt[x] + b[id]; }
void update(ll cur, ll cl, ll cr, ll id) {
  if (cl == cr) {
    if (calc(id, cl) < calc(segt[cur], cl))
      segt[cur] = id;
    return;
  }
  auto mid = (cl + cr) / 2;
  if (calc(id, mid) < calc(segt[cur], mid))
    swap(id, segt[cur]);
  if (calc(id, cl) < calc(segt[cur], cl))
    update(lson, cl, mid, id);
  else if (calc(id, cr) < calc(segt[cur], cr))
    update(rson, mid + 1, cr, id);
}
ll query(ll cur, ll cl, ll cr, ll x) {
  if (cl == cr)
    return calc(segt[cur], x);
  auto mid = (cl + cr) / 2;
  if (x <= mid)
    return min(calc(segt[cur], x), query(lson, cl, mid, x));
  else
    return min(calc(segt[cur], x), query(rson, mid + 1, cr, x));
  return 0;
}
int main() {
  cin >> n >> s;
  tn = n;
  for (int i = 1; i <= n; ++i) {
    cin >> t[i] >> c[i];
    unisumt[i] = sumt[i] = sumt[i - 1] + t[i];
    sumc[i] = sumc[i - 1] + c[i];
  }
  sort(unisumt + 1, unisumt + n + 1);
  tn = unique(unisumt + 1, unisumt + n + 1) - unisumt - 1;
  for (int i = 1; i <= n; ++i) {
    pos[i] = lower_bound(unisumt + 1, unisumt + tn + 1, sumt[i]) - unisumt;
  }
  b[0] = 1e18;
  for (int i = 1; i <= n; ++i) {
    dp[i] = min(s * sumc[n], query(1, 1, tn, pos[i])) + sumt[i] * sumc[i];
    k[i] = -sumc[i];
    b[i] = dp[i] + s * (sumc[n] - sumc[i]);
    update(1, 1, tn, i);
  }
  cout << dp[n] << endl;
  return 0;
}

这个题同样可以用 deque 的常规斜率优化方法处理，码量同样不大。但是在斜率变化不具有单调性的一些斜率优化问题中，相比起 cdq 和平衡树等数据结构，李超树的码量相对小得多。

习题：

【ZJOI2007】仓库建设

线段树优化建图

这是一个比较有趣的问题。

>

  1. 点到点连边

  2. 点到区间内的所有点连边

  3. 区间内的所有点到点连边

求单源最短路

双半群模型：线段树背后的数学模型

这里先插入群论基础的介绍，让各位对群论有一个基本的了解。

群论基础

最初，天地是一片混沌黑暗。所有的元素混在一起，不分彼此。

神说，要让所有元素都有办法分组。于是便有了集合 $\mathcal D$。

神看集合是好的，于是便留下了集合 $\mathcal D$。从此，所有的元素都被归进了这个集合里。

神看所有元素相互交错却又无法互相交流，于是便说，要有运算。于是便有了集合上的运算 $\times$

神发现，$\times$会创造出乐园中所没有的元素，这是不好的。于是便有了封闭性：$\forall\ a,b\in \mathcal D,\ a\times b \in \mathcal D$

神发现，$\times$的变换十分混乱，交换运算顺序结果就可能改变，于是便有了结合律：$a\times (b\times c) = (a \times b) \times c$

神看 $\times$ 是好的，于是便把 $\mathcal D$ 和 $\times$ 放在一起，得到了半群：$(\mathcal D,\ \times)$

神认为，需要有一个特别的元素，让它变得特殊，所有的元素和它运算后都不变。于是便有了单位元/幺元：$\exists\ e\in\mathcal D,\ s.t. \ \forall\ a\in\mathcal D，e\times a = a$

神看幺元是好的，于是便有了幺半群 $(\mathcal D,\ \times)$

神认为，元素需要有元素的逆，让运算后的结果可以变回原样。于是就为每个元素赋予了逆元：$\forall\ a\in\mathcal D,\ \exists\ a^{-1}\in\mathcal D,\ s.t.\ a\times a^{-1} = a^{-1} \times a = e$

神看逆元是好的，于是便有了群 $(\mathcal D,\ \times)$

至此，神创造了群。然而，神注意到，群中元素的运算，一旦交换了顺序，便会改变结果。于是神说，要有交换律：$a \times b = b \times a$

神看交换律是好的，于是便有了交换群 $(\mathcal D,\ \times)$ （自然也会有对应的交换半群）

至此，上帝创造了交换群/阿贝尔群。当然，上帝并未满足于此，但是受限于篇幅原因，上帝来不及创造环，域等代数结构了。于是，他便转生成了伽罗瓦。这便是新约的故事了。

双半群模型是高度抽象化后的线段树模型，来自lxl的一次演讲，这里用群论的语言描述如下：

有一个交换半群 $(\mathcal D,\ +)$，一个半群 $(\mathcal M,\ *)$，运算 $\times:\mathcal D \times \mathcal M \rightarrow \mathcal D$，它们满足：

  • 结合律：$\forall a \in \mathcal D,\ b,c\in \mathcal M,\ (a\times b)\times c = a\times (b*c)$

  • 分配律：$\forall a,b\in \mathcal D,\ c \in \mathcal M,\ (a+b)*c = a\times c+b\times c$

此时这两个集合以及这三种运算被称作一个双半群模型，可以记作$(\mathcal D,\mathcal M,+,*,\times)$。这样的模型是可以描述一切传统线段树问题的（之所以这里强调传统线段树，是因为李超线段树和 Segment Tree Beats 之类的变种线段树并不能用双半群模型的方式描述）。

事实上，这里的 $\mathcal D$ 即为线段树每个节点所维护的信息，在代码中我们用Info的类型表示，而 $\mathcal M$ 则为每个节点上维护的标记，我们用Tag类型表示。那么三个运算所描述的意义也就呼之欲出了：$+$ 描述节点之间的合并操作，$*$ 描述标记之间的合并操作，$\times$ 描述将标记作用在节点上的操作。这样三个运算的性质所对应的实际意义是显而易见的。

那么，实际上我们所需要做的事情只有这两步：

  1. 确定$\mathcal D,\mathcal M$

  2. 确定$+,*,\times$三种运算

当然这么说是站着说话不腰疼，绝大多数的题目的难点便在于如何构造这五个东西。通常来讲， $\mathcal D$ 和 $\mathcal M$ 的一些内容是题目中很容易便可以看出来的。于是我们便可以遵循一下的步骤来尝试构造双半群：

  1. 确定 $\mathcal D, \mathcal M$ 中的一部分

  2. 考虑怎么把标记合并到节点上，并考虑是否封闭，是否满足结合律和交换律

  3. 如果不封闭或无法构造合适的运算，考虑：是否可以增加节点上的信息（也就是改变 $\mathcal D$ 中元素的定义），让这三个运算封闭/满足双半群模型的限制条件。通常来讲这总是可以的。

  4. 不断重复3，直到$(\mathcal D,\mathcal M,+,*,\times)$变成一个合法的双半群模型。

到目前为止，双半群模型仍然是一个很抽象的概念。因此，我们在这里用三个题目举例子：【模板】线段树2，【NOIP2022】比赛，以及【模板】线段树3

【模板】线段树2

题目要求实现：区间加，区间乘，区间和查询

首先考虑 $\mathcal D$ 中的元素。很显然，$\mathcal D$ 中一定需要包括节点的区间和；另外，我们把节点的长度也放在 $\mathcal D$ 中考虑。换句话说，$\mathcal D$ 中的元素形如：$(sum,\ len)$ 。

接下来考虑标记，也就是 $\mathcal M$。显然加法和乘法不能共用标记，也就是说 $\mathcal M$ 中一定要包括区间的加法和乘法标记，形如：$(add,\ mul)$。

接下来考虑运算。$+$ 的构造十分显然，把 $sum$ 和 $len$ 分别加一加即可。在考虑标记的复合 $*$ 之前，我们需要先明确 $\times$ 也就是标记作用到节点上的操作。在处理这个题目的过程中，不免遇到一个问题：先加后乘还是先乘后加。理论上而言两者皆可，但实践上先乘后加更为合理。那么，$\times$ 的操作就是这样的：$(sum,\ len)\times(add,\ mul)=(mul\cdot sum,\ len)$

这样我们就可以构造标记的复合了。考虑标记的结合律，我们有：

从而：

显然这个操作不具有交换律。事实上标记的合并通常都不具有交换律。

到此为止，我们就好了这个双半群模型。这里似乎没有经历前面3的步骤，因为这个题目的构造较为简单，不需要很复杂的操作。

【NOIP2022】比赛（改编）

给定 $x,\ y$ 两个序列，要求实现以下操作：

  1. $x$ 上的区间赋值

  2. $y$ 上的区间赋值

  3. 标记历史版本

  4. 查询区间 $[l,\ r]$ 上 $x_i \cdot y_i$ 的历史版本和

照着前面的思路，我们先考虑 $\mathcal D$ 和 $\mathcal M$ 的构造。区间历史 $x_i\cdot y_i$ 和是一个很明确的信号，标志着 $\mathcal D$ 中一定包含了当前的区间 $x_i\cdot y_i$ 和与历史和，分别记作 sxy 和 s。区间长度依然视作 $\mathcal D$ 的一部分。那么现在Info中包括了三个成员。

然后考虑标记Tag。显然，对x和y的区间赋值一定是标记的一部分，记作cx和cy。

那么我们开始尝试构造三个运算。

$+$ 的操作依然显然，只需把每一位加一加即可。

$\times$ 的操作则复杂的多。先考虑对sxy的更新。在此，我们需要对cx和cy进行分类讨论。

  1. cx != 0 && cy != 0。在此条件下，显然 $\sum x_i y_i = len \cdot cx\cdot cy$。

  2. cx != 0 && cy == 0。在此条件下，有：$\sum x_i y_i = \sum cx\cdot y_i = cx \cdot \sum y_i$。于是我们需要把 $\sum y_i$ 加入到Info中，记作 sy。

  3. cx == 0 && cy != 0。同理，需要加入sx。

  4. cx == 0 && cy == 0。什么都不用动。

于是，到此为止，我们的Info包含了这些东西：s, sx, sy, sxy, len。

接下来考虑维护历史版本和 s 。首先考虑 $\times$ 中对历史版本和的维护方式。显然的，我们每次进行区间历史和的时候， s 会增加一份 sxy。

然后我们想象一下在一个节点上连续多次做区间历史和的操作，假定我们没有对 sxy 做任何的修改，那么相当于有一个系数 mxy 在不断自增。这个时候，如果要访问这个节点的子节点，那么势必要对子节点的 s 做出同样的修改，也就是说 mxy 将会作为标记的一部分被下传。可见，mxy 是需要加入到 Tag 中去的。

接着我们考虑如果对 sxy 做出修改了要如何下传标记维护 s 。显然的，我们依然要根据 cx 和 cy 做分类讨论。

  1. cx != 0 && cy != 0。此时 $\sum x_i y_i = len \cdot cx\cdot cy$ 。此后每次做区间历史和的时候，相当于在 len 前面的一个系数在增加 cx * cy，把这个系数记作 mlen

  2. cx != 0 && cy == 0。此时 $\sum x_i y_i = cx \cdot \sum y_i$ 。此时做区间历史和操作的时候，相当于在 sy 前面的一个系数在增加 cx，记作 my。

  3. cx == 0 && cy != 0。同样有一个系数，记作 mx。

  4. cx == 0 && cy == 0。退化到没有做修改的情况。

那么，到目前为止，Tag 就包括了这些元素：cx, cy, mxy, mx, my, mlen。到此为止，我们已经可以完整的构造出 $\times$ 的操作了。

最后考虑标记的合并 $$。事实上，通过前面的分类讨论，$$ 的操作已经呼之欲出了。

最后是三个操作的参考代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
Info merge(Info lhs, Info rhs) {
  return Info{.s = lhs.s + rhs.s,
              .sxy = lhs.sxy + rhs.sxy,
              .sx = lhs.sx + rhs.sx,
              .sy = lhs.sy + rhs.sy,
              .len = lhs.len + rhs.len};
}
Info merge(Info info, Tag tag) {
  info.s += tag.mxy * info.sxy + tag.mx * info.sx + tag.my * info.sy +
            tag.mlen * info.len;
  if (tag.cx && tag.cy) {
    info.sxy = tag.cx * tag.cy * info.len;
    info.sx = tag.cx * info.len;
    info.sy = tag.cy * info.len;
  } else if (tag.cx) {
    info.sxy = tag.cx * info.sy;
    info.sx = tag.cx * info.len;
  } else if (tag.cy) {
    info.sxy = tag.cy * info.sx;
    info.sy = tag.cy * info.len;
  }
  return info;
}
Tag merge(Tag pre, Tag cur) {
  if (pre.cx && pre.cy) {
    pre.mlen += cur.mxy * pre.cx * pre.cy + cur.mx * pre.cx + cur.my * pre.my +
                cur.mlen;
  } else if (pre.cx) {
    pre.my += cur.mxy * pre.cx + cur.my;
    pre.mlen += cur.mlen + cur.mx * pre.cx;
  } else if (pre.cy) {
    pre.mx += cur.mxy * pre.cy + cur.mx;
    pre.mlen += cur.mlen + cur.my * pre.cy;
  } else {
    pre.mlen += cur.mlen;
    pre.mx += cur.mx;
    pre.my += cur.my;
    pre.mxy += cur.mxy;
  }
  if (cur.cx)
    pre.cx = cur.cx;
  if (cur.cy)
    pre.cy = cur.cy;
  return pre;
}