本系列长期更新，全部更新完后会同步到知乎专栏

AES算法，一般指Rijndeal算法

简介

AES原本指的是一套标准FIPS 197，而AES算法一般指分组大小为128bits的Rijndeal算法，由比利时学者Joan Daemen和Vincent Rijmen提出。

AES与Rijndeal的区别

AES仅指分段为128位的Rijndeal算法，两种算法对比如下：

(Nr表示循环轮数，Nb表示分组大小，Nk表示密钥长度，Nb和Nk单位都是32bits)

Nr	Nb=4 (AES)	Nb=6	Nb=8
Nk=4	10 (AES-128)	12	14
Nk=6	12 (AES-192)	12	14
Nk=8	14 (AES-256)	14	14

加密

总体流程

图片来自链接，这张图是AES-128的流程，AES-192和AES-256除了加密轮数和密钥长度以外都是一样的

AES加密的整个过程是在一个4×4的字节矩阵上运作的，这个字节矩阵称作state。这个字节矩阵是由当前明文块处理得到的，简而言之就是把当前的16个字节按照4个字节一行排列成矩阵，比如说

1	0x00,0x01,0x02,0x03,0x04,0x05,0x06,0x07,0x08,0x09,0x0a,0x0b,0x0c,0x0d,0x0e,0x0f

处理后得到的矩阵就是

0x00,0x01,0x02,0x03,
0x04,0x05,0x06,0x07,
0x08,0x09,0x0a,0x0b,
0x0c,0x0d,0x0e,0x0f

加密前要先进行KeyExpansion，将原始的密钥扩展得到扩展密钥，原始密钥同样要做与上面一样的变换得到矩阵才能进行运算

然后是开始加密，按照上图中顺序调用如下四个轮函数：

AddRoundKey：轮密钥加运算，将当前的
ByteSub：字节变换 (S盒变换)
ShiftRows：行变换
MixColumns：列变换

4个轮函数都是在伽罗瓦域$GF(256)$上进行的。伽罗瓦域 (Galois Field) 是一个满足特定规则的集合，其中元素可以进行加减乘除，且运算结果也都是这个集合的元素，具体细节可以。

接下来分析四个轮函数

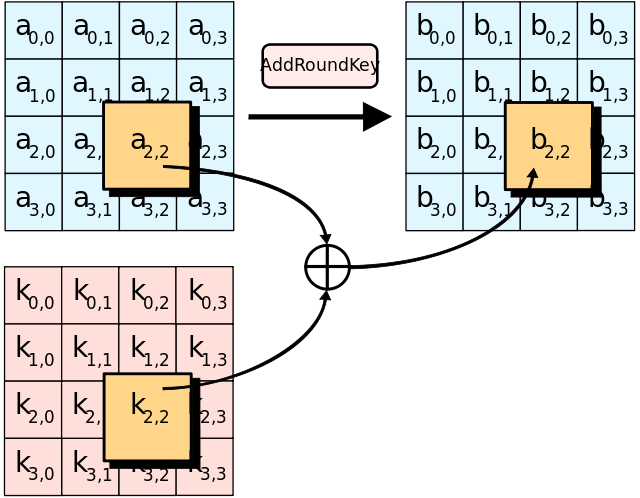
轮密钥加 / AddRoundKey

这个就是简单的把当前状态 (state) 与扩展密钥进行按位异或，代码如下：

void aes::AddRoundKey(word *ExpandedKey, int i) {
    toBytes(ExpandedKey[Nb * i + 0], RoundKey + 0 * Nb);
    toBytes(ExpandedKey[Nb * i + 1], RoundKey + 1 * Nb);
    toBytes(ExpandedKey[Nb * i + 2], RoundKey + 2 * Nb);
    toBytes(ExpandedKey[Nb * i + 3], RoundKey + 3 * Nb);
    for (int k = 0; k < Nb * 4; ++k) {
        state[k] = state[k] ^ RoundKey[k];
    }
}

注意：AddRoundKey所异或的扩展密钥与当前加密轮数有关。扩展密钥是一个word数组，每个word有32bit，也就是说每个word能分解为4个byte，而异或轮密钥的时候需要把当前要异或的一组轮密钥（共4个word）分解为16个byte再进行异或。扩展密钥的长度是Nb*(Nr+1)，每次AddRoundKey需要使用当前轮数乘上Nb开始的4个word长的轮密钥。

字节变换 / ByteSub

这一步就是将state中每一个字节替换为S_box中的对应字节。S_box是一个有256个元素的一维数组，直接查找当前字节所对应的新的字节并替换即可。

那肯定有人会问：S_box是怎么来的？

很显然这个S_box不是随随便便来的一个数组。这是通过计算得来的，当然我们直接把他看作一个常量数组即可。

S_box是怎么来的？

本段数学内容较多，可以直接跳到下一条分割线继续阅读。

首先我们要知道什么是$GF(256)$域，具体可以参考我的这篇文章。

(接下来默认你已经明白$GF(256)$和它上面的运算了)

首先我们求出当前字节在$GF(256)$上的乘法逆元 (相当于实数域上倒数的概念) ，如果当前字节是0x00则不变。我们把得到的这个数设为 $x$ 并把它以多项式的形式表示成如下形式：

$x_7a^7+x_6a^6+x_5a^5+x_4a^4+x_3a^3+x_2a^2+x_1a+x_0\qquad(a=2)$

接着我们有一个8位二进制数 $y$ ，同样以上面的方式表示，并且满足：

$\left[ \begin{array}{c} y_0\\y_1\\y_2\\y_3\\y_4\\y_5\\y_6\\y_7 \end{array} \right]= \left[ \begin{array}{cccccccc} 1\quad0\quad0\quad0\quad1\quad1\quad1\quad1\\ 1\quad1\quad0\quad0\quad0\quad1\quad1\quad1\\ 1\quad1\quad1\quad0\quad0\quad0\quad1\quad1\\ 1\quad1\quad1\quad1\quad0\quad0\quad0\quad1\\ 1\quad1\quad1\quad1\quad1\quad0\quad0\quad0\\ 0\quad1\quad1\quad1\quad1\quad1\quad0\quad0\\ 0\quad0\quad1\quad1\quad1\quad1\quad1\quad0\\ 0\quad0\quad0\quad1\quad1\quad1\quad1\quad1\\ \end{array} \right] \left[ \begin{array}{c} x_0\\x_1\\x_2\\x_3\\x_4\\x_5\\x_6\\x_7 \end{array} \right]+ \left[ \begin{array}{c} 1\\1\\0\\0\\0\\1\\1\\0 \end{array} \right]$

这个 $y$ 就是这个字节在S_box中所对应的值。

注意这里顺序是反的，高位在下低位在上，并且都是以2进制形式表示的

附上S_box数组：

const byte S_Box[256] = {
0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76,
0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0,
0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15,
0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75,
0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84,
0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf,
0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8,
0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2,
0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73,
0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb,
0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79,
0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08,
0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a,
0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e,
0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf,
0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16
};

行变换 / ShiftRow

这个就比较好理解了，就是把每行左环移，第一行不变，第二行环移1位，第三行环移2位，第三行环移3位，代码如下：

void aes::ShiftRow() {
    for (int i = 1; i < Nb; ++i) {
        for (int j = 0; j < i; ++j) {
            byte tmp = state[i];
            state[i + 0 * 4] = state[i + (0 + 1) * 4];
            state[i + 1 * 4] = state[i + (1 + 1) * 4];
            state[i + 2 * 4] = state[i + (2 + 1) * 4];
            state[i + 3 * 4] = tmp;
        }
    }
}

列混合 / MixColumn

这是整个AES加密流程中最复杂的一步，同时要应用到之前在S盒变换里提到过的GF(256)域，如果真的想要理解这一步的话建议先去仔细了解一下GF(256)再来继续阅读

我们定义一个多项式 $c(x)=’03’x^3+’01’x^2+’01’x+’02’$ ，带单引号的数表示16进制数。然后我们定义：

$b(x)=c(x)\otimes a(x)$

或者说

$\left[ \begin{array}{c} b_0\\b_1\\b_2\\b_3 \end{array} \right]= \left[ \begin{array}{cccc} 02\quad03\quad01\quad01\\ 01\quad02\quad03\quad01\\ 01\quad01\quad02\quad03\\ 03\quad01\quad01\quad02\\ \end{array} \right] \left[ \begin{array}{C} a_0\\a_1\\a_2\\a_3 \end{array} \right]$

得到了一个新的列。

但是实际上我们很少会直接用$GF(256)$上的乘法来计算这个。由于AES的整个加密和解密过程只需要用到256*6个GFMul的值，因此我们可以直接用查表的方式加速计算。

代码：

void aes::MixColumn() {
    const byte y[16] = {0x02, 0x03, 0x01, 0x01,
                        0x01, 0x02, 0x03, 0x01,
                        0x01, 0x01, 0x02, 0x03,
                        0x03, 0x01, 0x01, 0x02};
    byte arr[4];
    for (int i = 0; i < 4; ++i) {
        for (int k = 0; k < 4; ++k) {
            arr[k] = 0;
            for (int j = 0; j < 4; ++j) {
                arr[k] = arr[k] ^ GFMul(y[k * 4 + j], state[i * 4 + j]);
            }
        }
        for (int k = 0; k < 4; ++k) {
             state[i * 4 + k] = arr[k];
        }
    }
}

密钥扩展 / KeyExpansion

万事俱备，只欠东风。4个轮函数已经全部齐了，现在只差一步——密钥扩展。

扩展密钥是一个长为Nb*(Nr+1)的word数组，一个word相当于8个byte。对于AES-128和AES-192，代码如下：

void aes128::KeyExpansion() {
    for (int i = 0; i < Nk; ++i) {
        w[i] = toWord(key[4 * i], key[4 * i + 1], key[4 * i + 2], key[4 * i + 3]);
    }
    for (int i = Nk; i < Nb * (Nr + 1); ++i) {
        auto temp = w[i - 1];
        if (i % Nk == 0) {
            temp = SubByte(RotByte(temp)) ^ Rcon[i / Nk];
        }
        w[i] = w[i - Nk] ^ temp;
    }
}

而对于AES-256则多了一步：

void aes256::KeyExpansion() {
    for (int i = 0; i < Nk; ++i) {
        w[i] = toWord(key[4 * i], key[4 * i + 1], key[4 * i + 2], key[4 * i + 3]);
    }
    for (int i = Nk; i < Nb * (Nr + 1); ++i) {
        auto temp = w[i - 1];
        if (i % Nk == 0) {
            temp = SubByte(RotByte(temp)) ^ Rcon[i / Nk];
        } else if (i % Nk == 4) {
            temp = SubByte(temp);
        }
        w[i] = w[i - Nk] ^ temp;
    }
}

其中出现了几个东西：RotByte，SubByte和Rcon。

RotByte

RotByte函数是将这个word中的四个byte左环移一位，代码如下：

word aes::RotByte(crypto::word in) {
    word res;
    byte arr[4];
    toBytes(in, arr);
    res = toWord(arr[1], arr[2], arr[3], arr[0]);
    return res;
}

这个比较好理解，就不多说了。

SubByte

SubByte是对这个word里的每一个byte进行S盒变换，代码也很简单：

word aes::SubByte(crypto::word in) {
    word res;
    byte arr[4];
    toBytes(in, arr);
    res = toWord(S_Box[arr[0]], S_Box[arr[1]], S_Box[arr[2]], S_Box[arr[3]]);
    return res;
}

Rcon

这个就比较复杂了，仍然要用到$GF(256)$相关内容（当然我们也可以把它看作常数数组）

首先我们有一个数组RC，其中：

$RC[1]=1 \qquad RC[i]=2^{(i-1)}$

这里的所有运算都是在$GF(256)$上进行的。

而Rcon[i]=toWord(Rc[i],0x00,0x00,0x00)。

整个数组如下：

const word Rcon[16] = {0x00000000, 0x01000000, 0x02000000, 0x04000000,
                       0x08000000, 0x10000000, 0x20000000, 0x40000000,
                       0x80000000, 0x1b000000, 0x36000000, 0x6c000000,
                       0xd8000000, 0xab000000, 0xed000000, 0x9a000000};

解密

解密过程与加密过程刚好相反。这里只放几个关键数据：

逆S盒

const byte Inv_S_Box[256] = {
    0x52, 0x09, 0x6a, 0xd5, 0x30, 0x36, 0xa5, 0x38, 0xbf, 0x40, 0xa3, 0x9e, 0x81, 0xf3, 0xd7, 0xfb,
    0x7c, 0xe3, 0x39, 0x82, 0x9b, 0x2f, 0xff, 0x87, 0x34, 0x8e, 0x43, 0x44, 0xc4, 0xde, 0xe9, 0xcb,
    0x54, 0x7b, 0x94, 0x32, 0xa6, 0xc2, 0x23, 0x3d, 0xee, 0x4c, 0x95, 0x0b, 0x42, 0xfa, 0xc3, 0x4e,
    0x08, 0x2e, 0xa1, 0x66, 0x28, 0xd9, 0x24, 0xb2, 0x76, 0x5b, 0xa2, 0x49, 0x6d, 0x8b, 0xd1, 0x25,
    0x72, 0xf8, 0xf6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xd4, 0xa4, 0x5c, 0xcc, 0x5d, 0x65, 0xb6, 0x92,
    0x6c, 0x70, 0x48, 0x50, 0xfd, 0xed, 0xb9, 0xda, 0x5e, 0x15, 0x46, 0x57, 0xa7, 0x8d, 0x9d, 0x84,
    0x90, 0xd8, 0xab, 0x00, 0x8c, 0xbc, 0xd3, 0x0a, 0xf7, 0xe4, 0x58, 0x05, 0xb8, 0xb3, 0x45, 0x06,
    0xd0, 0x2c, 0x1e, 0x8f, 0xca, 0x3f, 0x0f, 0x02, 0xc1, 0xaf, 0xbd, 0x03, 0x01, 0x13, 0x8a, 0x6b,
    0x3a, 0x91, 0x11, 0x41, 0x4f, 0x67, 0xdc, 0xea, 0x97, 0xf2, 0xcf, 0xce, 0xf0, 0xb4, 0xe6, 0x73,
    0x96, 0xac, 0x74, 0x22, 0xe7, 0xad, 0x35, 0x85, 0xe2, 0xf9, 0x37, 0xe8, 0x1c, 0x75, 0xdf, 0x6e,
    0x47, 0xf1, 0x1a, 0x71, 0x1d, 0x29, 0xc5, 0x89, 0x6f, 0xb7, 0x62, 0x0e, 0xaa, 0x18, 0xbe, 0x1b,
    0xfc, 0x56, 0x3e, 0x4b, 0xc6, 0xd2, 0x79, 0x20, 0x9a, 0xdb, 0xc0, 0xfe, 0x78, 0xcd, 0x5a, 0xf4,
    0x1f, 0xdd, 0xa8, 0x33, 0x88, 0x07, 0xc7, 0x31, 0xb1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xec, 0x5f,
    0x60, 0x51, 0x7f, 0xa9, 0x19, 0xb5, 0x4a, 0x0d, 0x2d, 0xe5, 0x7a, 0x9f, 0x93, 0xc9, 0x9c, 0xef,
    0xa0, 0xe0, 0x3b, 0x4d, 0xae, 0x2a, 0xf5, 0xb0, 0xc8, 0xeb, 0xbb, 0x3c, 0x83, 0x53, 0x99, 0x61,
    0x17, 0x2b, 0x04, 0x7e, 0xba, 0x77, 0xd6, 0x26, 0xe1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0c, 0x7d
};

逆列变换

void aes::InvMixColumn() {
    const byte y[16] = {0x0e, 0x0b, 0x0d, 0x09,
                        0x09, 0x0e, 0x0b, 0x0d,
                        0x0d, 0x09, 0x0e, 0x0b,
                        0x0b, 0x0d, 0x09, 0x0e};
    byte arr[4];
    for (int i = 0; i < Nb; ++i) {
        for (int k = 0; k < 4; ++k) {
            arr[k] = 0;
            for (int j = 0; j < 4; ++j) {
                arr[k] = arr[k] ^ GFMul(y[k * 4 + j], state[i * 4 + j]);
            }
        }
        for (int k = 0; k < 4; ++k) {
            state[i * 4 + k] = arr[k];
        }
    }
}

逆行变换

void aes::InvShiftRow() {
    for (int i = 1; i < Nb; i++) {
        for (int j = 0; j < Nb - i; ++j) {
            byte tmp = state[i];
            state[i + 0 * 4] = state[i + (0 + 1) * 4];
            state[i + 1 * 4] = state[i + (1 + 1) * 4];
            state[i + 2 * 4] = state[i + (2 + 1) * 4];
            state[i + 3 * 4] = tmp;
        }
    }
}

轮密钥加和密钥扩展

加密和解密过程中轮密钥加和密钥扩展是完全一样的，不需要另外写新的代码。

参考资料：

matt-wu: AES

The Rijndeal Block Cipher