AES加密(3):AES加密模式与填充
AES有多种加密方式和填充方式。
加密方式
分组密码加密方式主要有7种:ECB,CBC,CFB,OFB和CTR,这五种方式将在下面一一讲解。
0. 初始化向量 / IV
在讲加密模式之前首先得要了解一个概念:初始化向量 (IV)
在除ECB以外的所有加密方式中,都需要用到IV对加密结果进行随机化。在使用同一种加密同一个密钥时不应该使用相同的IV,否则会失去一定甚至全部的安全性。如果到这里还不明白的话没关系,后面还会继续讲到。
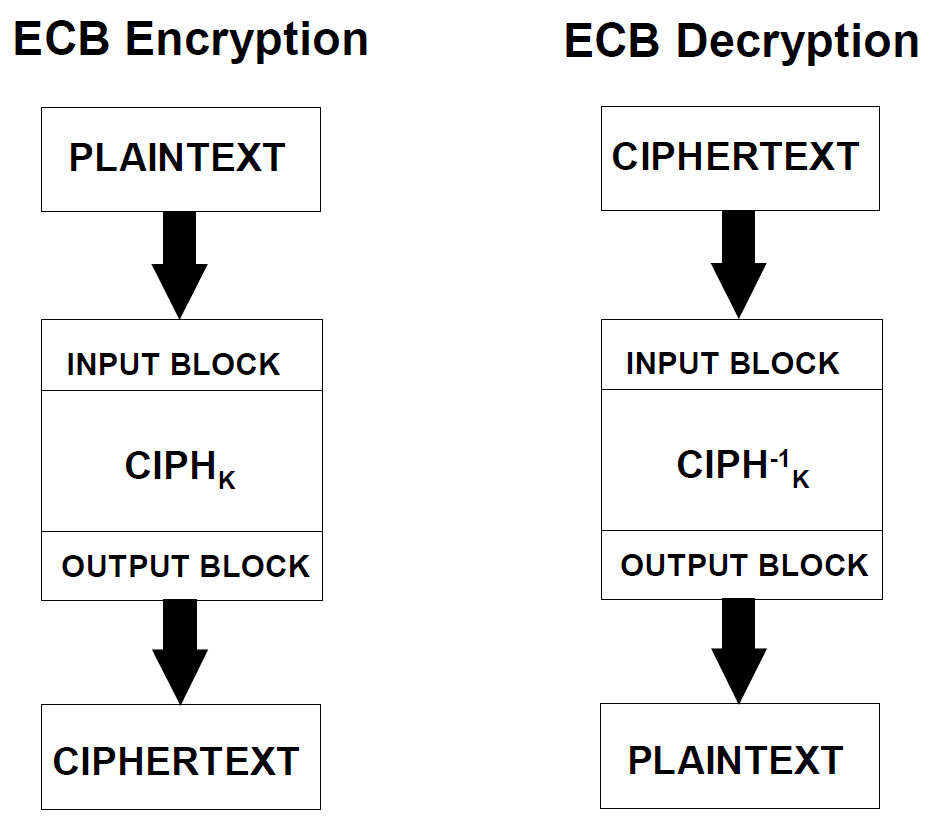
1. 电子密码本 / ECB
这里$CIPH$指AES加密算法,$CIPH^{-1}$指AES解密算法。
这个很好理解:将明文简单的按照128bit为一个分块进行切割,把每个分块分别进行AES加密,然后再将得到的密文简单的拼接一下即可。
注意到AES加密只能加密128bit的分块,那问题就产生了:如果明文的长度不是128bit的倍数,就会存在一个分块不足128bit,那如何对这个分块进行加密?
别慌,你想到的问题别人早就想到了。为了解决这个问题,我们发明了一种叫做填充的东西,这将会在后面具体讲解。OFB和CTR不需要填充!
ECB模式有一个显著的安全问题:如果使用相同的密钥,那么相同的明文块就会生成相同的密文块,不能很好的隐藏数据模式。这听起来没什么大事,但事实上这对数据安全是一个很大的威胁,下面这张图很明显的体现出了这个问题:
因此,在密码协议中不建议使用ECB模式。
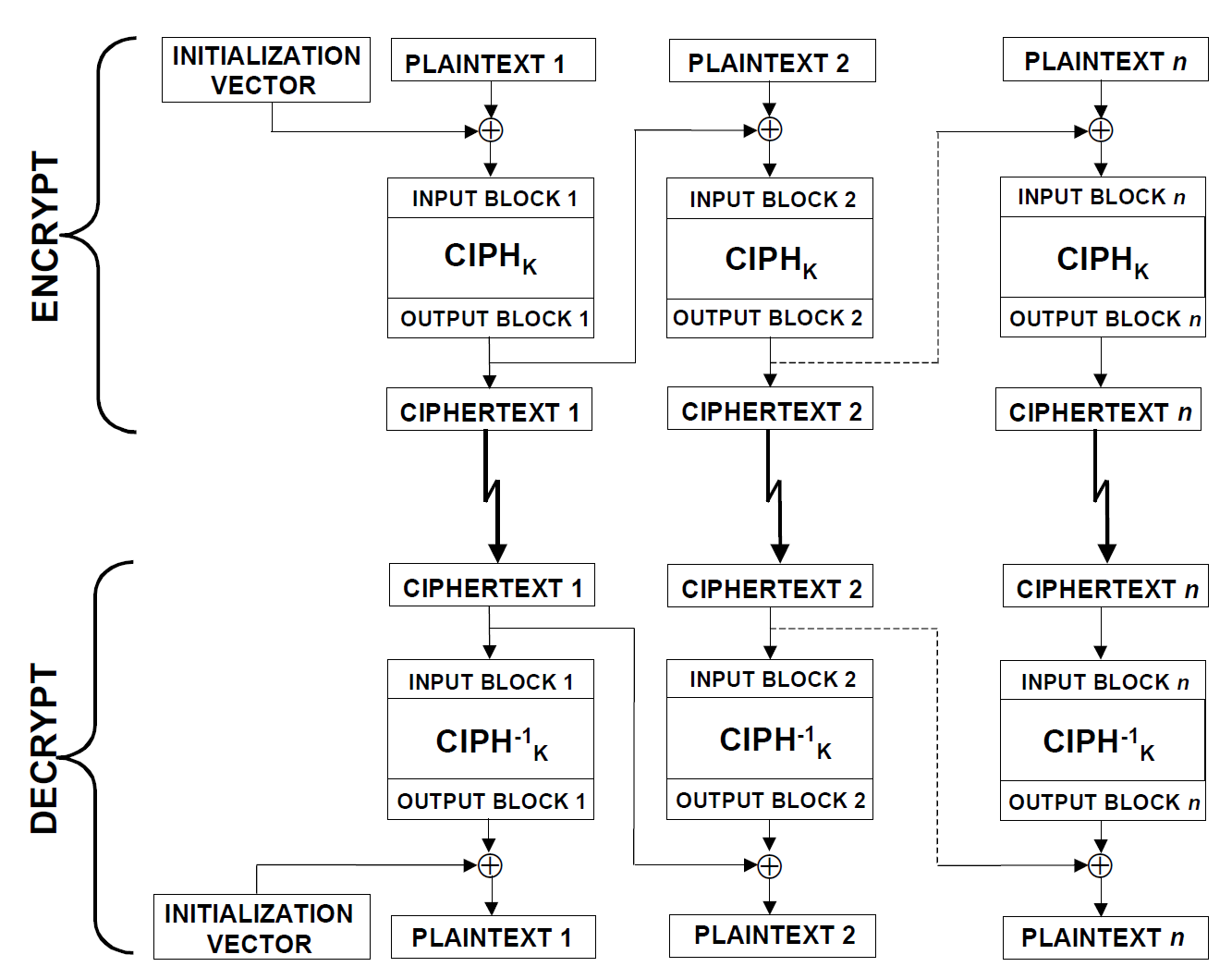
2. 密码块链接 / CBC
在CBC中,每个明文块要先与前一个密文块进行异或后再加密,每个密文块都依赖于前面的所有明文块。
那么问题又来了:第一个明文块怎么办?
这个时候就要用到IV了。在CBC中,IV先与第一个明文块进行异或,得到第一个明文块,然后再进行后续的加密。详见下图:
这个方法看起来很不错,但有一个缺点:加密过程是串行的,不能并行化,速度比较慢,但是解密可以并行。另外,如果密文的某一位被修改了,只会使这个密文块所对应的明文块完全改变并且改变下一个明文块的对应位,安全性仍然有一定的欠缺。
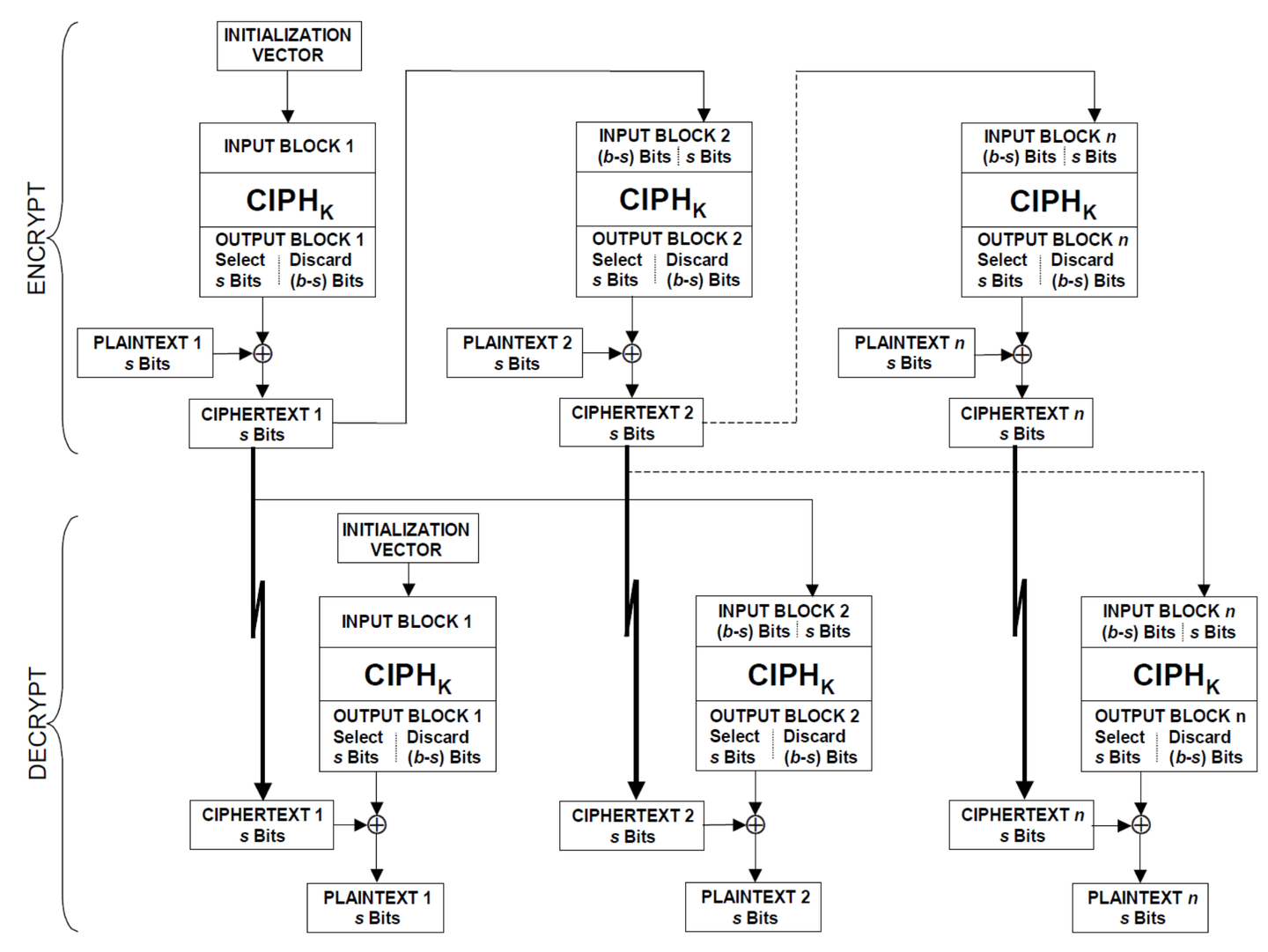
3. 密文反馈 / CFB
CFB的加密跟解密过程几乎完全相同,注意它在解密过程中使用的是AES加密而不是AES解密
接着我们细细来看下它的过程:
CFB模式可以说是5个模式里最为特殊的一个,它不仅使用了数据块,还另外引入了一个它所独有的“数据段”的概念。在其他的加密方式中,明文和密文都是以数据块进行“打包”来加密的,而在CFB中却是以“数据段”为单位进行操作。
我们来细细看看它的过程:
首先是将输入的IV作为第一个输入块进行AES加密,得到第一个输出块OUTPUT BLOCK1。仔细看图,我们发现,在这个输出块中,只取了它的前s bit的数据与第一个明文段进行异或操作。因此我们可以知道:数据段的长度一定会小于等于数据块的长度。常用的数据段长度有:1bit, 8bits 和128bits,因此CFB也分为CFB1、CFB8和CFB128,再分别跟三种AES算法组合,CFB加密总共有9种。
我们继续往下看,在OUTPUT BLOCK1中只取了前s bits与第一个明文段进行异或得到了第一个密文段,接着第一个密文段变成了第二个加密块的输入块的后S bits,那么问题来了:第二个块和后面的所有块的前(b-s)bits是从哪里来的?
我们注意到,在前一个加密块得到的密文块中,舍弃掉了后(b-s)bits,而这(b-s)bits就变成了后一个加密块的输入中的前(b-s)bits。
接下来又有一个十分反人类的问题:为什么在CFB的解密过程中使用的是加密算法而非解密算法?
这个问题看起来十分反常识,但实际上很好解释:密文段是由明文段与另一端信息进行异或得到的,那么也得要由原来的密文段异或上同样的一段信息才可以还原原来的明文段,而原来的那一段信息是由AES加密得到的,那么在解密过程中也要同样的进行加密才能算出这段内容以进行解密。
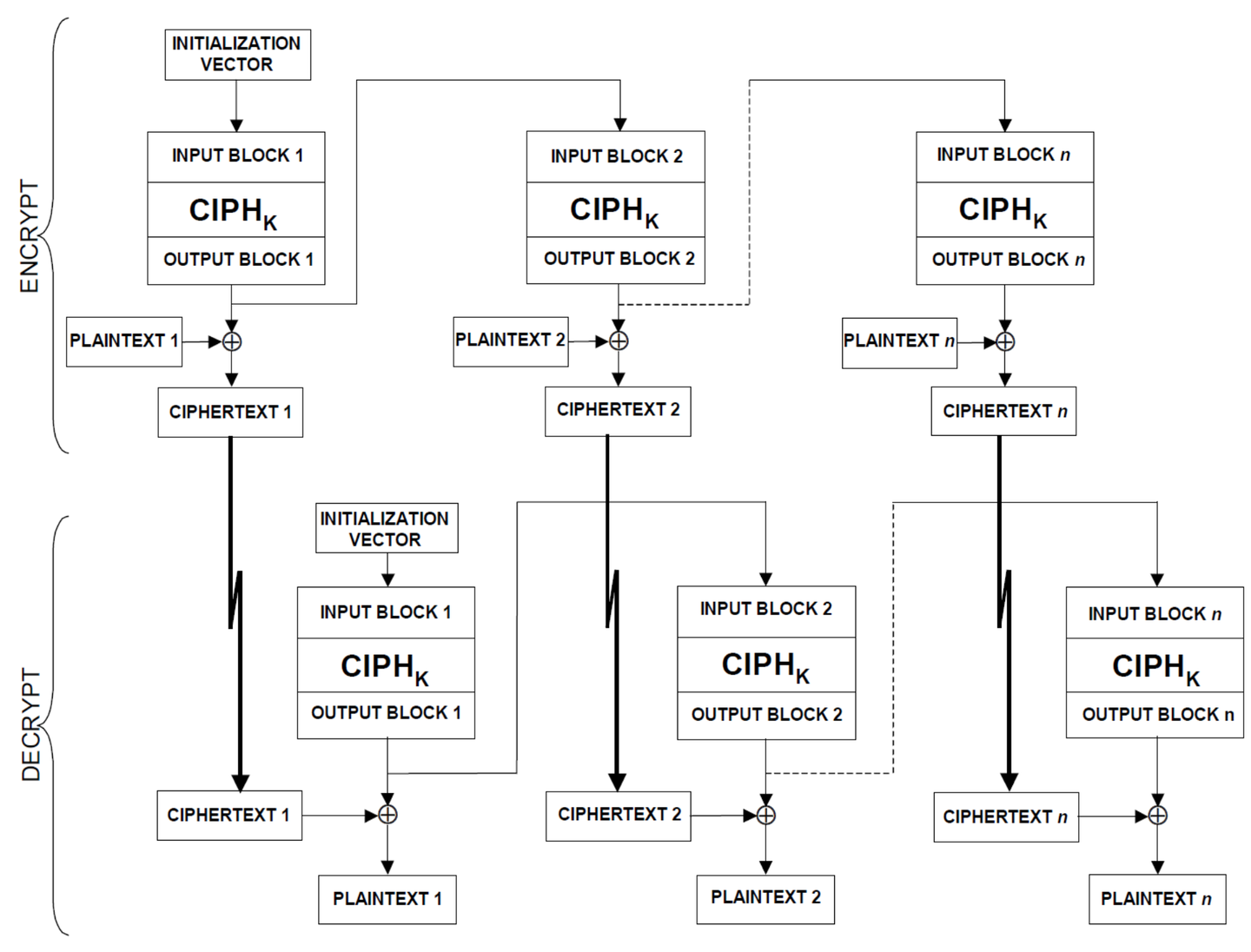
4. 输出反馈 / OFB
这个很简单,跟CFB128很相似,不同的是它是直接把输出块作为下一个块加密的输入块,具体看过程:
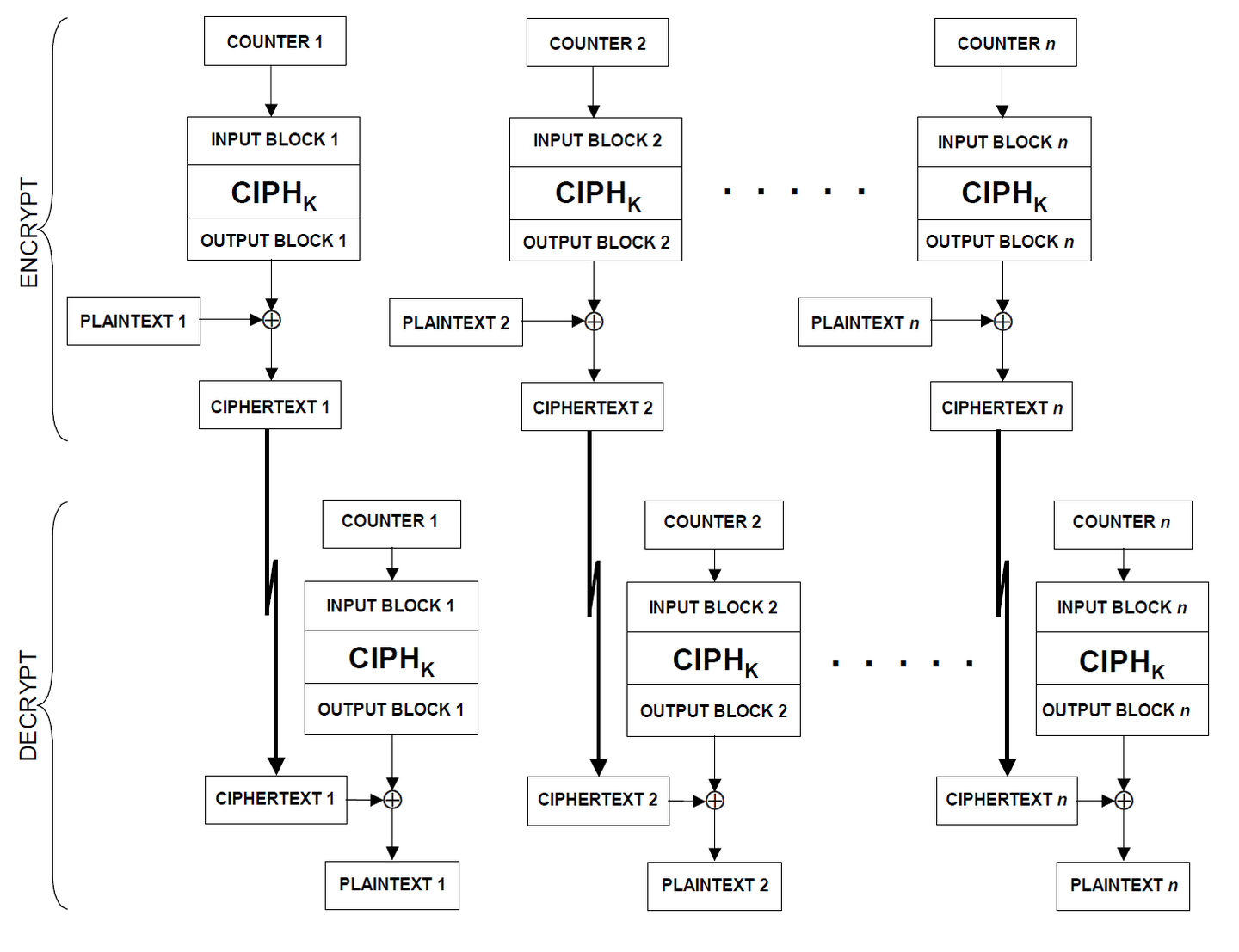
5. 计数器模式 / CTR
如下图
COUNTER是整个CTR模式的核心所在。它是由IV经过一定的规则之后生成的一段数据,长度与数据块的长度相等。接着我们要选定一个数m,这个m是用于确定计数器中累加部分的大小的,通常取块大小的一半,块大小是奇数就四舍五入(当然对于AES并没有这个问题)。初始的计数器COUNTER1是长度固定的任意一个随机字节序列,而不是像想象中那样一段随机数后面跟着一段0。
现在我们假设块大小b=8bits,m=5bits (这里只是为了便于举例才取8bits和5bits,在AES-CTR中通常是取16bytes和8bytes),我们用*表示随机值部分,初始计数器为***11110,那么最终计数器就是这样的:
1 | ***11110 |
也就是说,随机部分内容不变,其他部分每次+1,如果超出了范围就从0开始重新来。
网上很多都是说计数器是由nonce和counter组成,nonce和counter拼接组成计数器。这种说法其实本质上还是一样的,nonce就相当于这里counter的随机数部分,只不过我这里把两个合在一块讲了。
填充
填充有六种:NoPadding, PKCS#5, PKCS#7, ISO 10126, ANSI X9.23和ZerosPadding
NoPadding
顾名思义,就是不填充。缺点就是只能加密长为128bits倍数的信息,一般不会使用
PKCS#7 & PKCS#5
缺几个字节就填几个缺的字节数。
例子:
1 | ... | DD DD DD DD DD DD DD DD | DD DD DD DD 04 04 04 04 | |
注意:如果当前数据已经是128bits的倍数了也得要填充,否则无法解密。
对于AES来说PKCS5Padding和PKCS7Padding是完全一样的,不同在于PKCS5限定了块大小为8bytes而PKCS7没有限定。因此对于AES来说两者完全相同,但是对于Rijndael就不一样了。AES是Rijndael在块大小为8bytes时的特例,对于使用其他信息块大小的Rijndael算法只能使用PKCS7
2020.6.6更新:PKCS5的块大小是8bytes而AES的块大小是16bytes,所以实际上在AES加密中是不能使用PKCS5的,我们通常说的PKCS5和PKCS7就是同一个东西
(感谢知乎评论区提醒)
ZerosPadding
全部填充0x00,无论缺多少全部填充0x00,已经是128bits倍数仍要填充
例子:
1 | ... | DD DD DD DD DD DD DD DD | DD DD DD DD 00 00 00 00 | |
ISO 10126
最后一个字节是填充的字节数(包括最后一字节),其他全部填随机数
例子:
1 | ... | DD DD DD DD DD DD DD DD | DD DD DD DD 81 A6 23 04 | |
ANSI X9.23
跟ISO 10126很像,只不过ANSI X9.23其他字节填的都是0而不是随机数
例子:
1 | ... | DD DD DD DD DD DD DD DD | DD DD DD DD 00 00 00 04 | |
参考资料: